위치 기수법

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.

1. 개요
2. 역사
3. 표기법
- 3.1. 밑의 명시
4. 표준 위치 기수법
5. 비표준 위치 기수법
6. 진법 변환
7. 수의 표현과 유일성
8. 여러 기수의 혼합
9. p진수
참조

1. 개요

위치 기수법은 숫자를 나타내는 데 자리의 위치를 사용하는 기수법이다. 가장 널리 사용되는 십진법은 0부터 9까지의 숫자를 사용하며, 각 자릿수는 10의 거듭제곱을 나타낸다. 위치 기수법은 바빌로니아의 60진법, 아르키메데스의 십진법, 중국의 산가지 체계 등 고대 문명에서도 사용되었다.

위치 기수법은 덧셈 체계보다 실용적인 결과를 빠르게 얻을 수 있으며, 십진법 외에도 이진법, 8진법, 16진법 등 다양한 기수법이 존재한다. 십진법은 프랑스 혁명 이후 널리 확산되었으며, 10세기에는 알 우클리디시에 의해 십진 소수가 사용되었다. 위치 기수법은 음이 아닌 정수를 밑-1의 정수를 나열하여 나타내며, 소수점을 사용하여 분수를 표현할 수 있다. 이진법은 컴퓨터 과학에서 널리 사용되며, 음수 기수나 비표준적인 자릿수 집합을 사용하는 비표준 위치 기수법도 존재한다.

더 읽어볼만한 페이지

기수법 - 이진법
이진법은 0과 1 두 개의 숫자를 사용하는 밑이 2인 위치 기수법으로, 컴퓨터 과학의 기초가 되었으며 현대 컴퓨터에서 데이터를 저장하고 처리하는 데 사용된다.
기수법 - 구진법
구진법은 9를 밑으로 하는 위치 기수법으로 0부터 8까지의 숫자를 사용하여 수를 나타내며, 3의 배수 표현이 간결하고 3의 역수는 유한소수로 표현되는 특징이 있다.

위치 기수법
개요
유형	기수법
관련 개념	자리값
정의
기본 개념	밑 위치 기수법 비정수 기수법
숫자 체계
숫자 종류	바빌로니아 숫자 이집트 숫자 그리스 숫자 로마 숫자 마야 숫자 아라비아 숫자 한자 숫자
진법
주요 진법	단항 기수법 (1) 이진법 (2) 삼진법 (3) 사진법 (4) 오진법 (5) 육진법 (6) 팔진법 (8) 구진법 (9) 십진법 (10) 십일진법 (11) 십이진법 (12) 십오진법 (15) 십육진법 (16) 십팔진법 (18) 이십진법 (20) 삼십육진법 (36) 육십진법 (60)

2. 역사

오늘날 널리 사용되는 십진법은 열 손가락을 이용한 셈에서 비롯된 것으로 추정된다. 과거에는 다른 진법들이 사용되었고, 일부는 오늘날에도 계속 사용되고 있다.

위치 표기법이 표준이 되기 전에는 로마 숫자와 같은 간단한 덧셈 체계(기호값 표기법)가 사용되었으며, 고대 로마와 중세 시대의 회계사들은 산술을 하기 위해 주판이나 돌 계산자를 사용했다.^[4] 산가지와 대부분의 주판은 위치적 수 체계의 숫자를 나타내는 데 사용되었다.

프랑스 혁명(1789~1799) 이후, 새로운 프랑스 정부는 십진법 체계의 확장을 장려했다.^[5] 십진법 시간과 십진법 달력과 같은 십진법 지지 노력 중 일부는 성공하지 못했다. 통화 십진법화와 측정 단위의 미터법과 같은 다른 프랑스의 십진법 지지 노력은 프랑스에서 전 세계로 널리 확산되었다.

2. 1. 고대 문명의 기수법

오늘날 널리 사용되는 십진법은 열 손가락을 이용한 셈에서 비롯된 것으로 추정된다. 최초의 위치적 수 체계로 여겨지는 바빌로니아 수 체계는 60진법이었지만, 진정한 0은 없었다. 0은 기원전 700년경에 숫자 사이의 "공백"이나 "구두점 기호"(예: 두 개의 비스듬한 쐐기)로 나타내기 시작했으며,^[1] 숫자의 끝이나 단독으로 사용되지 않았기 때문에 진정한 0이라기보다는 자리 표시자였다. 2와 120(2×60)과 같은 숫자는 큰 숫자에 최종 자리 표시자가 없었기 때문에 동일하게 보였다.

아르키메데스(기원전 287~212년경)는 모래알 계산에서 10⁸을 기반으로 하는 십진법 위치 체계를 고안했다.^[2] 헬레니즘과 로마 천문학자들은 바빌로니아 모델을 기반으로 하는 60진법 체계를 사용했다.

위치 표기법이 표준이 되기 전에는 로마 숫자와 같은 덧셈 체계(기호값 표기법)가 사용되었으며, 고대 로마와 중세 시대의 회계사들은 산술을 하기 위해 주판이나 돌 계산자를 사용했다.^[4]

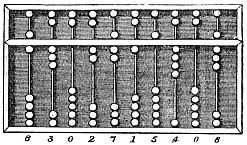
산가지와 대부분의 주판은 위치적 수 체계의 숫자를 나타내는 데 사용되었다.

2. 2. 동양의 기수법

오늘날 널리 사용되는 십진법(십진법) 체계는 아마도 열 손가락을 이용한 셈에서 비롯된 것으로 보인다. 과거에는 다른 진법들이 사용되었고, 일부는 오늘날에도 계속 사용되고 있다. 예를 들어, 최초의 위치적 수 체계로 여겨지는 바빌로니아 수 체계는 60진법이었다. 그러나 바빌로니아 수 체계에는 진정한 0이 없었다. 처음에는 문맥에서만 추론되었지만, 기원전 700년경에는 숫자 사이에 "공백"이나 "구두점 기호"(예: 두 개의 비스듬한 쐐기)로 0을 나타내게 되었다.^[1] 이것은 숫자의 끝이나 단독으로 사용되지 않았기 때문에 진정한 0이라기보다는 자리 표시자였다.

위치 표기법이 표준이 되기 전에는 로마 숫자와 같은 간단한 덧셈 체계(기호값 표기법)가 사용되었으며, 고대 로마와 중세 시대의 회계사들은 산술을 하기 위해 주판이나 돌 계산자를 사용했다.^[4]

산가지와 대부분의 주판은 위치적 수 체계의 숫자를 나타내는 데 사용되었다. 산가지나 주판을 사용하여 산술 연산을 수행할 때, 계산의 시작값, 중간값 및 최종값을 각 위치 또는 열에 간단한 덧셈 체계로 쉽게 작성할 수 있었다. 이 방법은 (위치 표기법과 같이) 표를 암기할 필요가 없었고 실용적인 결과를 빠르게 얻을 수 있었다.

가장 오래된 기존 위치 표기법 체계는 기원전 8세기 초부터 사용된 중국 산가지 체계이거나, 7세기에 위치적 숫자의 사용을 보여주는 크메르 숫자일 수 있다. 크메르 숫자와 다른 인도 숫자는 기원전 3세기경의 브라흐미 숫자에서 유래했는데, 당시에는 위치적으로 사용되지 않았다. 중세 인도 숫자는 위치적이며, 10세기부터 기록된 파생된 아라비아 숫자도 마찬가지이다.

2. 3. 근대 이후의 발전

프랑스 혁명(1789~1799) 이후, 새로운 프랑스 정부는 십진법 체계의 확장을 장려했다.^[5] 십진법 시간과 십진법 달력과 같은 십진법 지지 노력 중 일부는 성공하지 못했다. 그러나 통화 십진법화와 측정 단위의 미터법과 같은 다른 프랑스의 십진법 지지 노력은 프랑스에서 전 세계로 널리 확산되었다.

10세기 초 아랍 수학자 알 우클리디시는 처음으로 위치적 십진 소수를 사용했다.^[6] 1350년경 유대인 수학자 임마누엘 본필스는 십진 소수를 사용했지만, 이를 나타내는 표기법을 개발하지는 않았다.^[7] 15세기 페르시아 수학자 자무시드 알 카시는 십진 소수를 같은 방식으로 발견했다.^[6] 9세기 초 알콰리즈미는 이슬람 국가에 분수를 도입했는데, 그의 분수 표현 방식은 손자산경의 전통적인 중국 수학 분수와 유사했다.^[8] 분자를 위에, 분모를 아래에 수평선 없이 표기하는 이러한 분수 형태는 10세기 알 우클리디시와 15세기 자무시드 알 카시의 저서 "산술의 열쇠"에서도 사용되었다.^[8]^[9]

1보다 작은 수, 즉 분수의 십진 표현 채택은 사이먼 스테빈의 교과서 De Thiende를 통해 이루어진 것으로 알려져 있다.^[10] 그러나 스테빈과 E. J. 다이크스터후이스는 모두 레기오몬타누스가 일반적인 십진법의 유럽 채택에 기여했다고 지적한다.^[11]

3. 표기법

표준적인 기수법에서 음이 아닌 정수는 어떤 밑에 대하여 1부터 밑-1의 정수들을 자릿수만큼 나열하여 나타낸다. 예를 들어 밑이 10인 표준적인 위치 기수법을 10진법이라고 한다.^[12]

십진법에서는 열 개의 숫자를 사용하여, 한 자리에 하나의 숫자를 넣고 필요한 자릿수만큼 나열하여 수치를 나타낸다. 아라비아 숫자라면 '''0''', '''1''', '''2''', '''3''', '''4''', '''5''', '''6''', '''7''', '''8''', '''9''' 열 개이고, 한자라면 '''〇''', '''一''', '''二''', '''三''', '''四''', '''五''', '''六''', '''七''', '''八''', '''九''' 열 개이다. 예를 들어 십진법에서 '''312.02'''는

: $3\times 10^2+1\times 10^1 + 2\times 10^0 + 0\times \frac{1}{10^1}+2\times \frac{1}{10^2}$

을 나타낸다.

오진법을 아라비아 숫자로 표현하면 사용하는 숫자는 '''0''', '''1''', '''2''', '''3''', '''4''' 의 다섯 종류이며, 오진법에서의 '''431.02'''는

: $4\times 5^2+3\times 5^1 + 1\times 5^0 + 0\times \frac{1}{5^1}+2\times \frac{1}{5^2}$

을 나타내며, 이것은 십진법의 '''116.08'''에 해당한다.

12진법, 16진법, 20진법과 같이, ''N''이 10보다 큰 경우에는 아라비아 숫자만으로는 충분하지 않다. 따라서 10보다 큰 수를 표기하는 "숫자"로 라틴 문자의 알파벳 대문자를 사용하는 경우가 많다. 예를 들어 16진법이라면, "숫자"로서 '''0''', '''1''', '''2''', '''3''', '''4''', '''5''', '''6''', '''7''', '''8''', '''9''', '''A''', '''B''', '''C''', '''D''', '''E''', '''F''' 를 사용하며, '''A''', '''B''', '''C''', '''D''', '''E''', '''F'''는 각각 10진법의 자연수 10, 11, 12, 13, 14, 15에 해당한다. 따라서 예를 들어 '''2F3.A7'''은

: $2\times 16^2+15\times 16^1 + 3 + 10\times \frac{1}{16^1}+7\times \frac{1}{16^2}$

을 나타내며, 이것은 10진법의 '''755.652344'''에 해당한다.

위치 기수법은 기수의 거듭제곱을 이용하여 작동한다. 자릿수의 값은 자릿수에 자릿값을 곱한 값이다. 자릿값은 기수를 ''n''제곱한 값이며, 여기서 ''n''은 주어진 자릿수와 소수점 사이에 있는 다른 자릿수의 개수이다. 주어진 자릿수가 소수점 왼쪽에 있다면(즉, 값이 정수라면) ''n''은 양수 또는 0이고, 자릿수가 소수점 오른쪽에 있다면(즉, 값이 분수라면) ''n''은 음수이다.

밑수 ''b''의 음의 지수로 확장될 수 있다. 따라서 소위 소수점(주로 ».«)은 음이 아닌 지수를 갖는 자리와 음의 지수를 갖는 자리를 구분하는 데 사용된다. 정수가 아닌 숫자는 소수점 뒤에 자릿수를 사용한다. 소수점 뒤의 각 자리(즉, 일의 자리 뒤)에 대해, ''b''^''n''의 지수 ''n''은 1씩 감소하고, 그 거듭제곱은 0에 가까워진다. 예를 들어, 숫자 2.35는 다음과 같다.

: $2\times 10^0 + 3\times 10^{-1} + 5\times 10^{-2}$

밑과 모든 자릿수 집합이 음이 아닌 경우, 음수는 표현할 수 없다. 이를 극복하기 위해, 여기서는 »−«와 같은 빼기 부호가 수 체계에 추가된다. 일반적인 표기법에서는 음이 아닌 수를 나타내는 숫자열 앞에 붙인다.

비정수의 표현은 소수점 이후 무한한 숫자열을 허용하도록 확장할 수 있다. 무리수는 모든 정수 기수에서 무한하지 않고 반복되지 않는 표현을 갖는다. 유리수가 유한한 표현을 갖는지 또는 무한히 반복되는 표현을 필요로 하는지는 기수에 따라 달라진다.

순환소수에 대해, '''순환마디'''()를 윗줄 등으로 나타내는 표기법도 사용된다.^[29]

: $2.42\overline{314}_5 = 2.42314314314314314\dots_5$

이는 순환소수 표기법이다 (단일하게 전 세계적으로 받아들여지는 표기법이나 표현은 존재하지 않는다). 10진법에서는 순환소수 또는 순환십진소수라고 한다.

유리수를 소수로 나타낼 때, 유한소수가 되는 경우와 순환소수가 되는 경우가 있다. 일반적으로 기약분수 가 밑 의 위치 기수법에서 유한소수로 나타내어지려면, 분모 가 밑 이 가지는 소인수 $p_1,\, \dots,\, p_m$ 의 곱 $y = p_1^{k_1} {}\dotsb{} p_m^{k_m}$ (단, 는 이상의 정수) 이어야 한다.^[35]

3. 1. 밑의 명시

관례적으로, 특별히 언급이 없는 한, 위치 기수법으로 표시된 수는 십진수로 해석된다. 다른 진수를 사용하고 있음을 나타내기 위해 다음과 같이 진수를 함께 표기하는 경우가 있다.^[27]

:

{d_{m-1} \cdots d_1 d_0.d_{-1} d_{-2} \cdots d_{-\ell} \,}_{(N)} \,,

또는 진수를 괄호로 묶지 않고,

:

{d_{m-1} \cdots d_1 d_0.d_{-1} d_{-2} \cdots d_{-\ell} \,}_{N} \,,

혹은 수를 괄호로 묶어서,

:

\left(d_{m-1} \cdots d_1 d_0.d_{-1} d_{-2} \cdots d_{-\ell}\right)_{N}\,.

위의 표기법에서 진수 자체는 십진법으로 표기된다. 예를 들어,

10_{(2)}

는 이진수이며, 십진수

2

와 같은 수를 나타낸다. 또

100_{(16)}

는 십육진수이며, 십진수

256

과 같은 수를 나타낸다.

다른 표기법으로, 컴퓨터 프로그래밍에서 프로그래밍 언어에 따라, 정해진 수를 나타내는 구문(리터럴)이 준비되어 있다. 예를 들어 C언어나 C++에서는, 123은 십진법, 0x012abc 및 0X345DEF는 십육진법, 0b0101 및 0B1010은 이진법, 0123은 팔진법의 상수를 각각 나타내며, 진수의 구분은 선두 기호에 의해 이루어진다(0 이외의 숫자로 시작하면 십진수, 0x 또는 0X로 시작하면 십육진수, 0b 또는 0B로 시작하면 이진수, 그 이외는 팔진수로 해석된다)^[30]^[31]. 자바스크립트 등에서는 팔진수에 대해 더 엄격하게, 0o 또는 0O로 시작하는 문법을 채택하고 있다^[32].

4. 표준 위치 기수법

표준적인 기수법에서 음이 아닌 정수는 어떤 밑에 대하여 1부터 밑-1까지의 정수들을 자릿수만큼 나열하여 나타낸다. 밑 ''N''에 대하여 ''N''진법(base ''N'')으로 부른다. 예를 들어 밑이 10인 표준적인 위치 기수법을 10진법이라고 한다.^[12]

일반적으로 b진수에서 자릿수는 ''b''개이며, 숫자는 다음과 같이 표현된다.

: $(a_3 a_2 a_1 a_0)_b = (a_3 \times b^3) + (a_2 \times b^2) + (a_1 \times b^1) + (a_0 \times b^0)$

위치 기수법은 기수의 거듭제곱을 이용하여 작동한다. 자릿수의 값은 자릿수에 자릿값을 곱한 값이다. 자릿값은 기수를 ''n''제곱한 값이며, 여기서 ''n''은 주어진 자릿수와 소수점 사이에 있는 다른 자릿수의 개수이다. 주어진 자릿수가 소수점 왼쪽에 있다면(즉, 값이 정수라면) ''n''은 양수 또는 0이고, 자릿수가 소수점 오른쪽에 있다면(즉, 값이 분수라면) ''n''은 음수이다.

예를 들어, 7진수에서 숫자 465는 다음과 같다.

: $4\times 7^2 + 6\times 7^1 + 5\times 7^0 = 4\times 49 + 6\times 7 + 5\times 1 = 243$

즉, 465₇ = 243₁₀이다.

모든 기수 ''b''에 대해 10_''b'' = ''b''이다. 왜냐하면 10_''b'' = 1×''b''¹ + 0×''b''⁰이기 때문이다. 예를 들어, 10₂ = 2, 10₃ = 3, 10₁₆ = 16₁₀이다.

12진법, 16진법, 20진법과 같이, ''N''이 10보다 큰 경우에는 숫자를 표기하기 위해 라틴 문자의 알파벳 대문자를 사용하기도 한다.

표기법을 확장하여 선행 마이너스 부호를 통해 음수를 표현할 수 있다. 주어진 기수에 대해 모든 표현은 정확히 하나의 실수에 해당하며, 모든 실수에는 적어도 하나의 표현이 있다.

4. 1. 십진법

십진법(base-10) 힌두-아라비아 숫자 체계에서는 오른쪽부터 시작하는 각 자릿수가 10의 거듭제곱을 나타낸다. 첫 번째 자릿수는 10⁰(1), 두 번째 자릿수는 10¹(10), 세 번째 자릿수는 10²(100), 네 번째 자릿수는 10³(1000) 등이다.

소수점은 일반적으로 마침표 또는 쉼표를 사용한다. 소수점 오른쪽의 자릿수는 10의 음수 거듭제곱을 곱한 값이다. 소수점 오른쪽 첫 번째 자릿수는 10⁻¹(0.1), 두 번째 자릿수는 10⁻²(0.01) 등이다.

예를 들어, 10진수 2674는 다음과 같다.

:(2 × 10³) + (6 × 10²) + (7 × 10¹) + (4 × 10⁰)

:(2 × 1000) + (6 × 100) + (7 × 10) + (4 × 1)

십진법은 가장 친숙한 위치기수법이다. 십진법에서는 열 개의 숫자를 사용하여, 한 자리에 하나의 숫자를 넣고 필요한 자릿수만큼 나열하여 수치를 나타낸다.

아라비아 숫자는 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 열 개이고, 한자는 〇, 一, 二, 三, 四, 五, 六, 七, 八, 九 열 개이다. 십진법에서는 이러한 숫자들을 나열하여 수를 표현한다. 예를 들어, '''312.02'''는 3 × 10² + 1 × 10¹ + 2 × 10⁰ + 0 × (1/10)¹ + 2 × (1/10)²를 나타낸다.

4. 2. N이 10 미만인 경우

표준 위치 기수법에서 밑이 10보다 작은 경우, 0부터 밑-1까지의 숫자를 사용한다. 예를 들어, 오진법에서는 0, 1, 2, 3, 4의 다섯 가지 숫자를 사용한다. 오진법에서 431.02는 다음과 같이 표현된다.^[27]

:

4\times 5^2+3\times 5^1 + 1\times 5^0 + 0\times \frac{1}{5^1}+2\times \frac{1}{5^2}

이는 십진법의 116.08에 해당한다. 같은 숫자 배열이라도 밑에 따라 값이 달라지므로, 몇 진법인지 명시하는 것이 중요하다.

4. 3. N이 10을 초과하는 경우

12진법, 16진법, 20진법과 같이, ''N''이 10보다 큰 경우에는 아라비아 숫자만으로는 숫자를 표기하기에 충분하지 않다. 따라서 10보다 큰 수를 표기하는 "숫자"로 라틴 문자의 알파벳 대문자를 사용하는 경우가 많다.

예를 들어 16진법에서는 다음과 같은 "숫자"를 사용한다.

0	1	2	3	4	5	6	7	8	9	A	B	C	D	E	F
0	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15

여기서 A, B, C, D, E, F는 각각 10진법의 자연수 10, 11, 12, 13, 14, 15에 해당한다.

따라서 16진법에서 2F3.A7은

$2\times 16^2+15\times 16^1 + 3 + 10\times \frac{1}{16^1}+7\times \frac{1}{16^2}$

을 나타내며, 이것은 10진법의 755.652344에 해당한다.

5. 비표준 위치 기수법

비표준 위치 기수법은 밑수가 고정되어 있지 않거나 양수가 아니며, 자릿수 기호 집합이 음수 값을 나타낼 때 흥미로운 성질을 가진다. 이러한 시스템은 컴퓨터 과학자들에게 실용적 및 이론적 가치를 지닌다.^[22]

균형 삼진법은 밑수가 3이지만 자릿수 집합은 이다. ""은 -1과 같은 값을 가진다. 숫자의 부정은 1의 을 바꿈으로써 쉽게 형성된다. 이 시스템은 알려진 추의 최소 집합을 찾아 알 수 없는 추의 무게를 결정해야 하는 저울추 문제를 해결하는 데 사용할 수 있다. 1, 3, 9, ..., 3^''n''의 알려진 단위 무게를 사용하여 최대 1 + 3 + ... + 3^''n'' 단위까지의 알 수 없는 무게를 결정할 수 있다. 무게는 저울의 양쪽 어느 쪽에도 사용하거나 전혀 사용하지 않을 수 있다. 알 수 없는 무게와 같은 저울추에 사용되는 무게는 로, 빈 저울추에 사용되는 경우 1로, 사용되지 않는 경우 0으로 지정된다. 알 수 없는 무게 ''W''가 그 저울추에 3(3¹)과 다른 쪽에 1과 27(3⁰ 및 3³)으로 균형을 이루면, 10진수로의 무게는 25 또는 균형 3진법으로 101이다.

:

계승 수 체계는 가변적인 밑수를 사용하여 계승을 자릿값으로 제공한다. 이는 중국인의 나머지 정리와 잉여 수 체계 열거와 관련이 있다. 이 시스템은 사실상 순열을 열거한다. 이것의 파생물은 하노이의 탑 퍼즐 구성을 계산 시스템으로 사용한다. 탑의 구성은 구성이 발생하는 단계의 10진수 계산과 일대일 대응으로 만들 수 있으며 그 반대도 가능합니다.

10진수 등가	−3	−2	−1	1	2	3	4	5	6	7	8
균형 3진법	0	1		1	1	10	11	1	10	11	10
−2진법	1101	10	11	1	110	111	100	101	11010	11011	11000
팩토리오이드				10	100	110	200	210	1000	1010	1100

6. 진법 변환

수학적 표기법에서 기수를 나타낼 때는 일반적으로 문자 'b'를 기호로 사용하며, 이진수 시스템의 경우 'b'는 2와 같다. 기수를 나타내는 또 다른 일반적인 방법은 숫자 뒤에 '''십진수'''를 아래첨자로 표기하는 것이다. 1111011₂는 숫자 1111011이 2진수이며, 123₁₀(십진 표기법), 173₈(팔진법) 및 7B₁₆(십육진법)과 같음을 의미한다. 책이나 논문에서 처음에 숫자 기수의 약어를 사용할 때는 이후에 기수를 다시 표기하지 않는다. 이진수 1111011은 1111011₂와 같다고 가정한다.

기수 'b'는 "b진수"라는 구절로도 나타낼 수 있다. 따라서 이진수는 "2진수", 팔진수는 "8진수", 십진수는 "10진수" 등이다.

M진법으로 표현된 수를 N진법으로 변환하는 알고리즘(진수 변환 알고리즘)이 존재한다. 유클리드 호제법을 연속적으로 적용하거나, 반복적인 곱셈(호너 방법)을 통해 기수 변환을 수행할 수 있다. 소수를 다른 N진법으로 변환하는 방법도 존재한다.

기수법에서 $b_1$ 진법으로 표현된 정수 $n$ 을 $b_2$ 진법으로 변환하는 것은 $b_2$ 로의 유클리드 호제법을 연속적으로 적용하여 수행할 수 있다. $b_2$ 진법에서 가장 오른쪽 자릿수는 $n$ 을 $b_2$ 로 나눈 나머지이고, 두 번째 오른쪽 자릿수는 몫을 $b_2$ 로 나눈 나머지이며, 이런 식으로 계속된다. 가장 왼쪽 자릿수는 마지막 몫이다. 일반적으로 오른쪽에서 $k$ 번째 자릿수는 $(k-1)$ 번째 몫을 $b_2$ 로 나눈 나머지이다.

예를 들어, 16진수 A10B_Hex를 10진수(41227)로 변환하는 과정은 다음과 같다.

0xA10B/10 = 0x101A R: 7 (일의 자리)
0x101A/10 = 0x19C R: 2 (십의 자리)
0x19C/10 = 0x29 R: 2 (백의 자리)
0x29/10 = 0x4 R: 1 ...
4

더 큰 진법으로 변환할 때(예: 2진수를 10진수로 변환), 나머지는

b_1

의 자릿수를 사용하여

b_2

를 한 자릿수로 나타낸다. 예를 들어, 2진수 0b11111001을 10진수 249로 변환하는 과정은 다음과 같다.

0b11111001/10 = 0b11000 R: 0b1001 (0b1001 = 일의 자리 "9")
0b11000/10 = 0b10 R: 0b100 (0b100 = 십의 자리 "4")
0b10/10 = 0b0 R: 0b10 (0b10 = 백의 자리 "2")

소수 부분의 경우, 소수점 이후의 자릿수(분자)를 취하고, 목표 기수에서의 암시적 분모로 나누어 변환할 수 있다. 기약분수의 분모가 변환할 기수의 소인수가 아닌 다른 소인수를 가지는 경우 무한소수가 될 가능성이 있으므로 근사값이 필요할 수 있다. 예를 들어, 10진수 0.1(1/10)은 2진수로 0b1/0b1010이며, 이를 해당 기수로 나누면 0b0.00011이 된다(10의 소인수 중 하나가 5이기 때문).

호너 방법을 사용하여 반복적인 곱셈을 통해 기수 변환을 수행할 수 있으며, 이는 반복적인 나눗셈과 동일한 계산 복잡도를 가진다.^[14] 위치 표기법의 수는 각 자릿수가 계수인 다항식으로 생각할 수 있다. 계수는 한 자릿수보다 클 수 있으므로, 기수를 변환하는 효율적인 방법은 각 자릿수를 변환한 다음, 호너 방법을 사용하여 목표 기수 내에서 다항식을 계산하는 것이다. 각 자릿수를 변환하는 것은 간단한 검색표이므로 비용이 많이 드는 나눗셈이나 모듈 연산이 필요하지 않다. 그리고 x를 곱하는 것은 오른쪽 시프트가 된다.

예: 0xA10B를 41227로 변환하는 과정은 다음과 같다.

A10B = (10*16^3) + (1*16^2) + (0*16^1) + (11*16^0)

검색표:

16진법	10진법
0x0	0
0x1	1
...	...
0x9	9
0xA	10
0xB	11
0xC	12
0xD	13
0xE	14
0xF	15

0xA10B의 10진수 자릿수는 10, 1, 0, 11이다.
자릿수를 배열한다. 가장 중요한 자릿수(10)는 "내린다".
10 1 0 11 <- 0xA10B의 자릿수
---------------
10
원본 기수(16)의 아래쪽 숫자를 곱하고, 그 곱은 원본 값의 다음 자릿수 아래에 배치한 다음 더한다.
10 1 0 11
160
---------------
10 161
최종 덧셈이 수행될 때까지 반복한다.
10 1 0 11
160 2576 41216
---------------
10 161 2576 41227
결과는 10진수 41227이다.

0b11111001을 249로 변환한다.

검색표:

2진법	10진법
0b0	0
0b1	1

결과:

1 1 1 1 1 0 0 1 <- 0b11111001의 자릿수
2 6 14 30 62 124 248
-------------------------
1 3 7 15 31 62 124 249

주어진 비음의 정수 ''T''를 기호

\mathfrak{c}_0,\ldots, \mathfrak{c}_{N-1}

을 숫자로 사용한 ''N''진법 표기

a_r\cdots a_0

로 나타내려면 다음 알고리즘을 사용하면 된다.

이 알고리즘은 ''M'' ≠ ''N''이므로 ''M''진법으로 표현된 ''T''를 ''N''진법으로 바꿀 때 자주 사용되므로, 이 알고리즘을 '''진수 변환 알고리즘'''이라고 부른다.

입력 ''T''를 받는다.
''T=0''이면 $\mathfrak{c}_0$ 을 출력하고 종료한다.
i를 0으로 초기화한다.
while(T≠0){
* ''T''를 ''N''으로 나눈 몫을 ''T''' , 나머지를 ''k''로 하고, $a_i\gets\mathfrak{c}_k$ 로 한다.
* ''T'' ←''T''' , i←i+1
}
r←i-1
$a_r\cdots a_0$ 을 출력한다.

''T'' >0에 대해서는 다음과 같은 등식이 성립한다.

r=\left\lfloor\log_N T\right\rfloor

(단, 첨자를 0부터 시작하므로 ''T''의 자릿수는 ''r'' +1이다). 여기서

\left\lfloor x \right\rfloor

는 바닥 함수이다.

;십진법→오진법으로의 변환

십진법의 5213을 오진법으로 바꾸는 경우, 5로 나누어서 몫이 5 미만이 될 때까지 계속한다. 나머지가 없는 경우에는 0을 명기한다. 몫이 5 미만이 되면, 마지막 몫을 선두로 하고, 첫 번째 나머지를 말미로 하여 나열한다.

5213 ÷ 5 = 1042 나머지 3
1042 ÷ 5 = 208 나머지 2
208 ÷ 5 = 41 나머지 3
41 ÷ 5 = 8 나머지 1
8 ÷ 5 = 1 나머지 3
1 ÷ 5 = 0 나머지 1

따라서, 5213 = 3 + 2 × 5 + 3 × 5² + 1 × 5³ + 3 × 5⁴ + 1 × 5⁵가 되므로, 오진법 표기에서는 131323으로 나타낼 수 있다. 또, 5⁵ = 3125, 5⁶ = 15625이므로, 5⁵ ≤ 5213 < 5⁶이 성립하므로, 로그를 취하면

5 \le \log_{5}5213 < 6

이 되고,

r=\left\lfloor\log_{5}5213\right\rfloor =5

를 알 수 있다.

;십진법 이외→십진법 이외로의 변환

십진법 이외의 N진법도 마찬가지로, 예를 들어 3⁸에 해당하는 육진법의 50213을 십육진법으로 바꾸는 경우에도, 몫이 24₍₆₎ = 10₍₁₀₎을 밑돌 때까지 24로 나누어 간다.

50213 ÷ 24 = 1522 나머지 1
1522 ÷ 24 = 41 나머지 14
42 ÷ 24 = 1 나머지 13

이상으로부터, 1, 13, 14, 1의 열이 되고, 13₍₆₎ = 9₍₁₀₎, 14₍₆₎ = A₍₁₆₎이므로, 십육진법에서는 19A1이 된다.

;동치의 소수로의 변환

소수를 다른 N진법으로 변환하는 경우에는, 다음 과정을 밟는다.

# 변환 전과 변환 후의 거듭제곱을 열거한다.

# 소수점 이하의 원래 자릿수에 맞춰, 거듭제곱을 곱한다.

# 반올림을 한다.

# 정수와 마찬가지로, 거듭제곱을 곱한 결과를, 변환 후의 N으로 나누어 간다.

# 변환 후의 N으로 나눈 결과를 마지막 상→첫 번째 나머지 순으로 열거한다. 이 열이 동치의 소수가 된다.

(예) 십진수 0.531441 → 십이진수 6자리

# 십진수 1000000 → 2985984 (십의 6승 → 십이의 6승)

# 531441×2.985984 = 1586874.322944

# 1586874.322944 → 1586874

# 1586874÷12 = 132239 나머지 6

#* 132239÷12 = 11019 나머지 11

#* 11019÷12 = 918 나머지 3

#* 918÷12 = 76 나머지 6

#* 76÷12 = 6 나머지 4

# 11₍₁₀₎ = B₍₁₂₎이므로, 6463B6₍₁₂₎을 나열한다.

이상으로부터, 십진수 0.531441은, 십이진수에서는 약 0.6463B6이 된다.

(예) 십진수 0.124053 → 육진수 9자리

# 십진수 1000000 → 10077696 (십의 6승 → 육의 9승)

# 124053×10.077696 = 1250168.42189

#* 변환 전의 소수가 6자리이므로, 승수도 소수점 이하를 6자리로 한다.

# 1250168.42189 → 1250168

# 1250168÷6 = 208361 나머지 2

#* 208361÷6 = 34726 나머지 5

#* 34726÷6 = 5787 나머지 4

#* 5787÷6 = 964 나머지 3

#* 964÷6 = 160 나머지 4

#* 160÷6 = 26 나머지 4

#* 26÷6 = 4 나머지 2

# 42443452₍₆₎를 나열한다. 분모가 10077696₍₁₀₎ = 1000000000₍₆₎이므로, 소수점 이하는 9자리가 되고, 선두에 0이 하나 추가된다.

따라서, 십진수 0.124053은, 육진수에서는 약 0.042443452가 된다.

7. 수의 표현과 유일성

선행 마이너스 부호를 허용하여 표기법을 확장하면 음수를 표현할 수 있다. 주어진 기수에 대해 모든 표현은 정확히 하나의 실수에 해당하며, 모든 실수에는 적어도 하나의 표현이 있다. 유리수의 표현은 유한하거나, 막대 표기법을 사용하거나, 무한히 반복되는 자릿수의 순환으로 끝나는 표현이다.

비정수의 표현은 소수점 이후 무한한 숫자열을 허용하도록 확장할 수 있다. 예를 들어, 3진법에서 1.12112111211112 ...는 다음과 같은 무한 급수의 합을 나타낸다.

: $\begin{array}{l}1\times 3^{0\,\,\,} + {}\\1\times 3^{-1\,\,} + 2\times 3^{-2\,\,\,} + {}\\1\times 3^{-3\,\,} + 1\times 3^{-4\,\,\,} + 2\times 3^{-5\,\,\,} + {}\\1\times 3^{-6\,\,} + 1\times 3^{-7\,\,\,} + 1\times 3^{-8\,\,\,} + 2\times 3^{-9\,\,\,} + {}\\1\times 3^{-10} + 1\times 3^{-11} + 1\times 3^{-12} + 1\times 3^{-13} + 2\times 3^{-14} + \cdots\end{array}$

무한한 숫자열 전체를 명시적으로 쓸 수 없으므로, 뒷부분의 생략 부호(...)는 생략된 숫자들을 나타내며, 이 숫자들은 어떤 패턴을 따를 수도 있고 따르지 않을 수도 있다. 일반적인 패턴 중 하나는 유한한 숫자열이 무한히 반복되는 경우이다. 이는 반복되는 블록 위에 상선을 그어 표시한다.^[16]

: $2.42\overline{314}_5 = 2.42314314314314314\dots_5$

이는 순환소수 표기법이다 (단일하게 전 세계적으로 받아들여지는 표기법이나 표현은 존재하지 않는다). 10진법에서는 순환소수 또는 순환십진소수라고 한다.

무리수는 모든 정수 기수에서 무한하지 않고 반복되지 않는 표현을 갖는다. 유리수가 유한한 표현을 갖는지 또는 무한히 반복되는 표현을 필요로 하는지는 기수에 따라 달라진다. 예를 들어, 1/3은 다음과 같이 나타낼 수 있다.

: $0.1_3$

: $0.\overline3_{10} = 0.3333333\dots_{10}$

: 또는, 기수를 생략하면:

: $0.\overline3 = 0.3333333\dots$ (0.999... 참조)

: $0.\overline{01}_2 = 0.010101\dots_2$

: $0.2_6$

최대공약수가 (''p'', ''q'') = 1인 정수 ''p''와 ''q''에 대해, 분수 ''p''/''q''는 ''q''의 각 소인수가 ''b''의 소인수이기도 할 때에만 기수 ''b''에서 유한한 표현을 갖는다.

주어진 기수에 대해, 유한한 개수의 숫자로 (상선 표기법을 사용하지 않고) 나타낼 수 있는 모든 수는 하나 또는 두 개의 무한 표현을 포함하여 여러 개의 표현을 갖는다.

유한하거나 무한한 개수의 0을 추가할 수 있다.

:

3.46_7 = 3.460_7 = 3.460000_7 = 3.46\overline0_7

마지막 0이 아닌 숫자를 1만큼 줄이고, 각각 기수보다 1 작은 값에 해당하는 무한한 숫자열을 추가할 수 있다 (또는 다음에 오는 0을 대체할 수 있다).

:

3.46_7 = 3.45\overline6_7

:

1_{10} = 0.\overline9_{10}\qquad

(0.999... 참조)

:

220_5 = 214.\overline4_5

(실)무리수는 모든 정수 기수에서 무한히 반복되지 않는 표현을 갖는다.^[17]

예시로는 해를 구할 수 없는 ''n''제곱근

:

y = \sqrt[n]{x}

(

y^n = x

이고 )와 같이 대수적인 수, 또는

:

\pi,e

와 같이 초월적인 수가 있다. 초월수의 개수는 비가산이며, 유한한 수의 기호로 이들을 적는 유일한 방법은 기호 또는 유한한 기호열을 부여하는 것이다.

이 절에서는 특별히 언급하지 않는 한 십진수에 대해 설명하지만, 다른 진수에 대해서도 마찬가지이다.

실수의 N진 표기는 유일하지 않다.

잘 알려져 있듯이,

:'''1'''='''1.000'''…='''0.999…'''

이다. 또한, 다음과 같이 상위 자릿수에 불필요한 '''0'''을 추가할 수도 있다.

:'''0013'''='''13'''

일반적으로 "'''0013'''"과 같은 표기는 허용하지 않는 경우가 많지만, 컴퓨터 등에서는 최대 4자릿수의 정수값임을 나타내기 위해 일부러 "'''0013'''"과 같은 표기를 하는 경우가 있다.

이와 같은 예외를 제외하면 '''0이 아닌''' 실수는 유일하게 표현할 수 있다.

그러나 0만은

: "'''+0'''", "'''-0'''"

의 두 가지 표기가 가능하다(소위 '''음의 영''' 문제). 이것이 원인이 되어 컴퓨터 프로그램에서는 '''0'''에 대해서만 예외 처리가 필요한 경우가 있다.

또한, 일반적으로 0은 1자릿수의 수로 간주되지만, 규칙을 우선하여 1자릿수의 수로 인정하지 않는 경우도 있다(복면산#규칙).

스프레드시트의 열 이름 등에 사용되는 A, B, ..., Z, AA, AB, ... 와 같은 형식은, 자릿수 기수법의 일종으로 생각할 수 있으며, 0보다 큰 정수를 유일하게 표현할 수 있다.

8. 여러 기수의 혼합

십진법에서는 십 배, 백 배, 천 배, 만 배 순으로 증가한다. 마찬가지로 십이진법에서는 십이 배, 백사십사 배, 천칠백이십팔 배, 이만칠천삼십육 배 순으로 증가한다.

하지만, 기수를 두 가지로 나누는 경우가 있다. 십진법에 대해, 이오진법(십이 오진법에서 "이오"와 구별하기 위해 이와 오 사이에 점이 필요하다)에는 이와 오의 두 가지 기수가 있으므로, 자릿수가 올라갈 때마다 오 배→이 배→오 배→이 배로 번갈아 가며, "십의 거듭제곱"과 "십의 거듭제곱의 오 배"가 번갈아 나타난다. 이것은 주판과 마찬가지로 한 자릿수가 "일의 자리" 넷과 "오의 자리" 하나로 구성되는 방법이며, 계산기에도 응용되고 있다.

시간의 경우 다음과 같이 여러 기수가 혼합되어 사용된다.

단위	사용되는 진법
초	육십진법
분	육십진법
시	이십사진법
일	칠진법 (주) 또는 삼십진법 (월)
월	십이진법
년	십진법
십년	십진법
세기	십진법
천년	십진법

바빌로니아의 육십진법도 주판과 비슷한 방법으로, 한 자릿수가 "일의 자리" 아홉 개와 "십의 자리" 다섯 개로 구성되어 있으며, 정수는 십 배→육 배→십 배→육 배로 번갈아 가며, 소수는 육분의 일→십분의 일→육분의 일→십분의 일로 번갈아 간다. 이 방법에서는 정수 두 번째 자리는 "육십의 자리"와 "육백의 자리"로 나뉘고, 정수 세 번째 자리는 "삼천육백의 자리"와 "삼만육천의 자리"로 나뉘며, 소수 첫 번째 자리는 "육분의 일의 자리"와 "육십분의 일의 자리"로 나뉘고, 소수 두 번째 자리는 "삼백육십분의 일의 자리"와 "삼천육백분의 일의 자리"로 나뉘어져 있다.

이러한 이·오진법이나 육십진법처럼 여러 개의 기수가 설정되어 있는 경우에는, ":"와 같은 구분 기호를 붙인다. 예를 들어, 육십진법에서 십진법을 보조로 사용하는 경우에는 58 → 59 → 1:00 → 1:01 → 1:02 … 순으로 수열이 진행된다.

일본의 통화(화폐와 지폐)는 일 엔→오 엔→십 엔→오십 엔→백 엔→오백 엔→천 엔→오천 엔→만 엔 순으로 증가하므로, 통화를 하나의 단위로 보면 이·오진법이라고 할 수 있다. 이 배열을 보면 일(10⁰), 십(10¹), 백(10²), 천(10³), 만(10⁴)이 십의 거듭제곱이며, 오, 오십, 오백, 오천이 "십의 거듭제곱의 오 배"이다.

9. p진수

'''N'''진법과 관련이 깊은 개념으로, 소수 '''p'''마다 정해지는 '''p'''진수라는 것이 있다. 명칭은 본 문서에서 설명하고 있는 '''N'''진법의 다른 이름인 '''N'''진수와 동일하지만, 별개의 개념이다. 다만, 양자는 매우 관련이 있으며, 정수의 '''p'''진법 표기를 (가산) 무한 자릿수의 자연수 범위로 확장한 것이 '''p'''진 정수이고, 거기에 유한 자릿수의 소수 부분을 허용한 것이 '''p'''진수이다. 단, "무한 자릿수의 정수"(일부는 유리수로 재해석할 수 있지만 대부분은)는 본 문서에서 다루는 보통의 수(실수)와는 다르다.^[1]

참조

_[1] 서적 The Nothing That Is: A Natural History of Zero https://archive.org/[...] Oxford University Press
_[2] 웹사이트 Greek numerals http://www-gap.dcs.s[...] 2016-05-31
_[3] 서적 Zahlwort und Ziffer. Eine Kulturgeschichte der Zahl Vandenhoeck und Ruprecht
_[4] 문서 Ifrah, page 187
_[5] 웹사이트 Sketch of The Analytical Engine Invented by Charles Babbage http://www.fourmilab[...] 2008-09-15
_[6] 서적 The Mathematics of Egypt, Mesopotamia, China, India, and Islam: A Sourcebook Princeton University Press
_[7] 간행물 The invention of the decimal fractions and the application of the exponential calculus by Immanuel Bonfils of Tarascon (c. 1350)
_[8] 간행물 The Development of Hindu-Arabic and Traditional Chinese Arithmetic
_[9] 학술지 A Chinese Genesis, Rewriting the history of our numeral system
_[10] 서적 A History of Algebra. From Khwarizmi to Emmy Noether https://archive.org/[...] Springer-Verlag
_[11] 서적 Simon Stevin: Science in the Netherlands around 1600 Martinus Nijhoff Publishers
_[12] 문서 The digit will retain its meaning in other number bases
_[13] 문서 We do not usually remove the lowercase digits "l" and lowercase "o"
_[14] 서적 Computer Algebra: Symbolic and Algebraic Computation Springer
_[15] 문서 The exact size of the does not matter.
_[16] 웹사이트 Vinculum https://mathworld.wo[...] 2024-08-22
_[17] 웹사이트 Irrational Numbers: Definition, Examples and Properties https://flamath.com/[...] 2024-04-10
_[18] 서적 Mathematical Cuneiform Texts https://books.google[...] American Oriental Society and the American Schools of Oriental Research 2019-09-18
_[19] 학술지 Making the Old Way Count http://www.ankn.uaf.[...] 2017-02-27
_[20] 서적 Pi in the sky: counting, thinking, and being https://archive.org/[...] Clarendon Press
_[21] 백과사전 Encyclopedia of Indo-European Culture
_[22] 문서 Knuth, pages 195–213
_[23] 문서 Ifrah, pages 326, 379
_[24] 문서 Ifrah, pages 261–264
_[25] 서적 新明解国語辞典三省堂
_[26] 서적 Science and civilisation in China. Pt. 1: Vol. 5. Chemistry and chemical technology Paper and printing Cambridge Univ. Pr 2001
_[27] 웹사이트 Base
_[28] 웹사이트 Negative
_[29] 웹사이트 Vinculum
_[30] 웹사이트 Integer literal https://en.cpprefere[...] 2023-03-16
_[31] 웹사이트 Integer constant https://en.cpprefere[...] 2023-03-16
_[32] 웹사이트 MDN web docs - 字句文法 # 数値リテラル https://developer.mo[...] 2023-03-16
_[33] 웹사이트 A Simple Overview of Smalltalk Syntax https://www.gnu.org/[...] 2023-03-16
_[34] 웹사이트 Data Types https://www.erlang.o[...] 2023-03-16
_[35] 웹사이트 Regular Number

본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com